01交互式多准则(Multi-Crieria)优化任务的优化库
文章链接:交互式多准则优化库 再加上Opotimizatin说明书
机构:德国航空航天中心系统动力学与控制研究所
期刊:第九届国际Modelica会议论文集
指数:⭐⭐(技术层面,但这个工具给人感觉没有特别好用,仅限modelica使用,没啥拓展性)
文章摘要:
提供了几种数值优化算法,用于解决不同类型优化任务
(技术开发原因)
数值优化算法在工程中应用广泛,例如系统设计等等,但其中的数值算法成为使用的阻碍,如何开发一种易于操作的优化受到了搭建的关注。
(与此相关的项目)
OMOptim是一个在OpenModelica中提供开源优化平台的项目,不过该平台主要借助遗传算法进行优化,而本文拟在提供各种不同的优化算法解决不同的优化问题。
Jmodelica拓展Optimica也用于解决动态优化问题,Optimica定义了额外的Modelica语言元素用来直接在Modelica描述优化问题,因此需要特殊编译器来优化运行生成代码。
design.Optimization是本篇文章的前身,对其用户界面进行了增强。
(过程介绍)
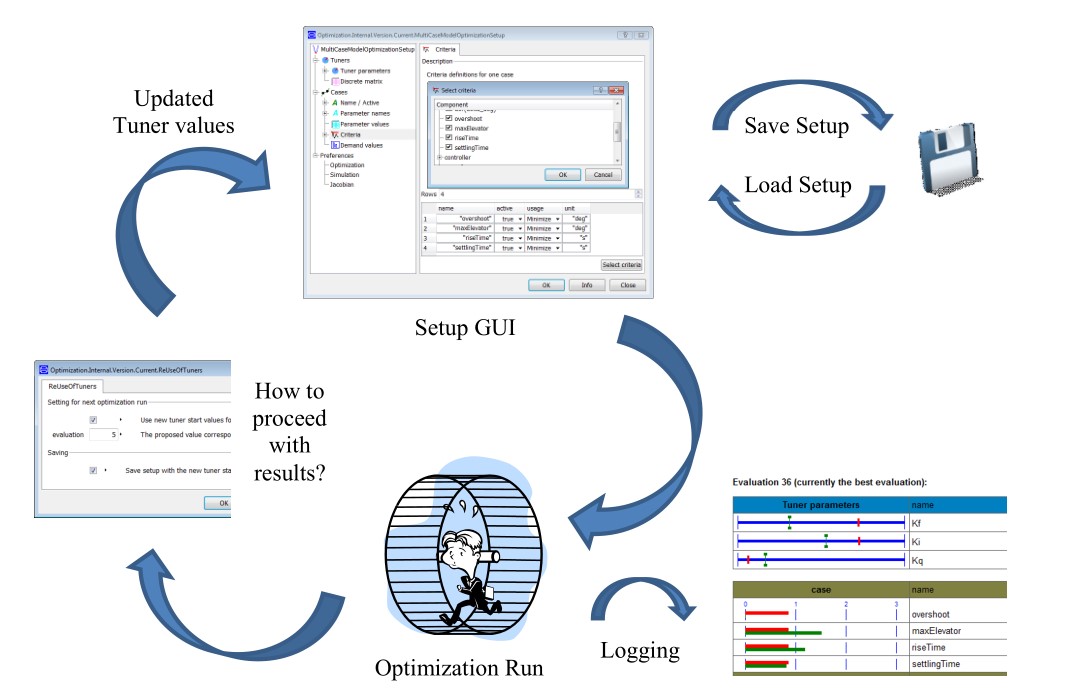
无论是哪一种任务,其处理过程都是一样的,包括4个部分,优化任务的配置、启动优化、优化结果的展示、优化结果的保存与更新。
在任务的配置这一部分,需要分层完成任务列表的配置,包括优化变量、优化算法、模型雅可比矩阵指定方法等等,所有的信息在设置完成之后都可以保存在Modelica文件中。
之后点击ok便可以开始运行,相同的,在dymola命令框中也可以通过调用函数也可以。在优化运行期间,当前的解决方案会将记录在html文件中,并且也会在Dymola命令行窗口显示。各种功能都是为了交互体验,让用户知道现阶段算法在干什么。
最后,还会有一个纯数值数据的记录文件,可以用来重置优化变量。
(优化问题中一些概念的介绍)
优化问题一般能写成如下格式:
其中:
(基于函数的优化)
(这一部分我觉得并不是重点,应该属于一个开发前期的工作,得有但不常用的功能)
Function based Optimization中包含两种任务模式,一种是Function Optimization,另一种是Realtime Optimization。
Function Optimizattion是指用户指定目标函数,然后运行计算,其中并不涉及模型,使用时,声明待校准参数、校准目标等设置,需要注意的是,一些基于梯度的算法中需要使用到梯度,系统会默认使用对称有限差分(双面数值差分,计算量大,但相对于单边差分准确性提高大),如果提前知道解析解,也可以直接输入梯度。
Realtime Optimization是一种在模型中调用优化函数的模式,比如在模型运行到10min时,需要对设定值进行优化更新,之后再次输入到模型中,被用于汽车的模型预测控制。
(基于模型的优化)
Model based Optimization是Optimization模型库的重点部分,解决基于Modelica模型的数值积分的优化任务,其中又能细分为四种任务模式,Model Optimization、Multi Case Model Optimization、Trajectory Optimization。
首先提到了其创建的 Criteria 模型库,这部分没有什么新奇的,就是对信号的处理,例如计算最大值、计算最小值、计算累计值之类的模块。
Model Optimization用于优化Modelica模型中的某些参数,使用方法就不去介绍了,需要注意的是,我打开库尝试了一下,发现其也无法指定雅可比矩阵,只能依赖单向或者双向差分的方法获取雅可比矩阵数值解,从而用于优化工作中。
Multi Case Model用于同时优化多种工况下模型参数,例如当一个控制器既用于A建筑,又用于B建筑(AB建筑模型结构完全一致,只是少数几个参数不同),需要同时考虑该控制器在两个建筑中的运行效果,这时候就可以使用Multi Case Model,它会指定每一个目标的权重。
Trajectory Optimization适用于轨迹优化,例如建筑需求响应中,想要使得建筑电耗为特定曲线,需要优化得到对应的控制点设定值,这就是轨迹优化问题,从原理上来说,轨迹优化问题应当是一个无限维优化问题,也就是说优化得到的应该是一个时间映射函数,但这一点很难,因此Optimization库中采用的方法是利用样条插值的方法来实现,利用几个点来描述一个轨迹,同样也有有限几个点来描述设定点优化值。
Periodic Steady State Initialization(这一种在文章中并未说明,但库中存在)比较神奇的一种方式,用于解决初始化问题,优化初始值,使得模型某一段时间后状态量与设定值保持一致,优化部分用到的方法就是Model Optimization,只是在生成优化问题这一步是自动化执行的,自动识别状态量与状态量初值。
(模型优化中的并行问题)
模型在优化过程中可以利用并行运行加快优化速度,Optimization利用OpenMP程序实现这一功能,但需要注意的是,并行并不一定可以带来速度的提升,速度取决于两个部分,一个是模型的顺序读写处理部分,另一个是模型运行部分,对于单线程来说,数据的顺序读写与处理是较块的,而对于多线程来说,可以让多个线程同时运行多个模型,因此在模型计算速度上多线程占优势,而在数据读写与处理上单线程占优势,文章中的测试表明,如果模型单次运行时间在1s以内,单线程优势明显,模型在1s以上,多线程优势明显。此外,多线程运行什么也是一个关键,有两种,一种是多线程处理雅可比举证(这一部分耗时长),另一种多线程处理多个案例模型。在Optimization中可以设置。
补充说明
Optimization是商业库,使用时会出现许可问题。
代表图片

02面向OpenModelica的设计优化,强调遗传算法的参数优化
文章链接:OpenModelica的优化包
机构:巴黎科技矿业公司能源与过程中心
期刊:第八届国际Modelica会议论文集
指数:⭐⭐(技术层面,偏向于Modelica用户使用,解决的是开源问题)
文章摘要:
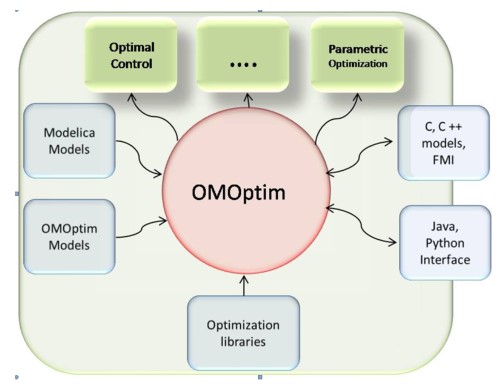
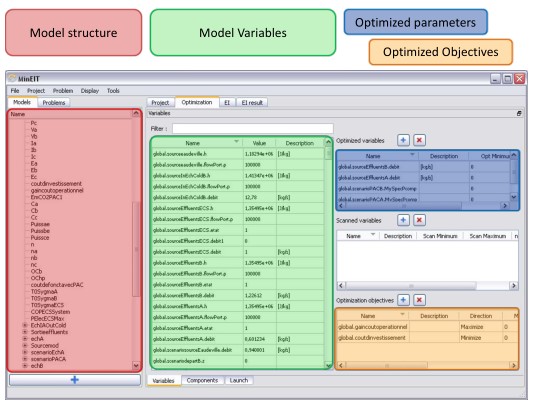
介绍了OMOptim优化平台,主要是搭建一个台子,一方面方便使用者进行优化,另一方面方便开发人员开发相关算法,文章中介绍,想要解决两个问题,一个问题是开源平台的问题,想要不仅开源且方便使用,另一个是优化速度问题。
文章中将优化方法分为两大类,基于梯度的方法与基于启发算法,认为基于梯度的算法会带来数值上的麻烦,启发式算法研究火热。
然后介绍了一下界面、架构以及测试案例。
最后说了下以后的畅想与同类产品的介绍,想要1)实现将优化以模块的形式放入平台中,2)实现混合求解算法,3)在模型运行时进行优化,4)并行开发,5)优化性能分析以及程序调试。与他相关的产品包括:Dymola Optimization、Jmodelica Optimica、Gneopt、Isight。
给我的感觉像是想集几个软件于大成,Genopt的开放性与智能算法、Optimization的并行与用户界面,但还没了解过现在是怎样的。
代表图片:
03使用 Optimica 和 JModelica.org 进行建模和优化 – 用于解决大规模动态优化问题的语言和工具
介绍了如何对modelica模型描述的系统进行优化,有很多基础知识的介绍,收获很大
文章链接:使用Optimica和 JModelica.org 进行建模和优化 – 用于解决大规模动态优化问题的语言和工具 – ScienceDirect
机构:隆德大学自动控制系
期刊:计算机与化学工程(Computers &Chemical Engineering)
指数:⭐⭐⭐⭐
文章摘要
(开发背景)
由于目前系统或者设备产品的复杂性提到,无论是规模上还是结构上,因此人的计算是难以满足的,仿真工具,结构化的建模工具随之出现。
随着进一步的发展,仿真模型的作用也会发生改变,不再单纯的作为一个预演器(看看系统运行结果)去使用,我们需要借助仿真模型去对系统进行优化,需要完成包括模型仿真、参数敏感性分析、设计优化、控制系统开发与部署等等,这就需要更加灵活、操作性更强的工具与算法来实现这件事情。
这篇文章对假想研究对象进行了说明,抛弃Fortran、C这样的建模方式,他们将以Modelica为建模语言,特点是针对优化问题制定了数值求解算法(使得用户能够利用较为高级的语言来描述整个优化问题),但另一方面,利用轻量级的语言描述设定优化算法与控制参数,使得不同算法能够很轻易的被测试使用。
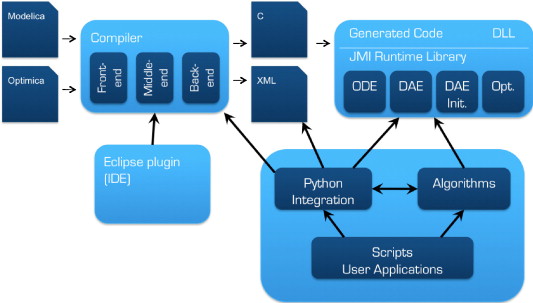
这一项目将命名为Optimica,并且开发了Jmodelica.org平台,是一个Modelica开源平台,致力于创建一个灵活可拓展的Modelica环境,其前端可以将Modelica与Optimica代码转化为特定表达形式,后端生成高效代码(C与XML格式),并且提供Python接口,目标算法为基于梯度的方法,但也适合与启发式算法结合使用。
(建模技术背景)
这一部分介绍Modelica的特点,面向对象、组件建模、非因果建模、连接器……这些概念就不多说,但提到一点(虽然知道,但很重要),Modelica语言是不适合与数值求解算法直接集成的,Modelica语言需要进行进一步转化才能适合求解计算,其步骤包括:1)将Modelica代码转化为方程与变量的表达;2)利用结构与符号算法,将混合DAE转化为结构化形式;3)利用排序算法将DAE进行最后的整理(之前感觉这应该就是一个因果化过程);4)生成底层代码(C)供数值算法集成。
(动态优化背景)
我们处理的问题大多属于动态问题(例如需求响应追踪电功率等等),在这篇文章种,并没有提到太多对动态优化问题的介绍,这一部分需要有最优控制的基础,在这里放一些可能有用的文章链接:
基于模型的化学过程在移动视界上的优化简介 (researchgate.net)
动态过程优化同步策略的进展 – 科学直接 (sciencedirect.com)
最优控制问题数值方法-直接法/打靶法 (1) – 知乎 (zhihu.com)
在这篇文章中提到了三种方法,首先时贝尔曼提出的最优性原理,表明动态规划的有效性,也就出现了“哈密尔顿-雅可比-贝尔曼方程”(HJB方程),其次是最大原理,在文章中有这样一句话“动态规划提供了闭环控制定律(作为系统状态函数的控制定律),而最大原理则为开环控制定律(作为时间函数的控制定律)提供了最优的必要条件”,(对此目前还没有说明理解),再然后说明两种方法在处理大规模方程时存在问题,于是出现了新的方法,直接法,将无限维的动态问题转录为有限维静态优化问题来解决动态优化问题,两条主要的方法,一种顺序方法(控件通常通过分段多项式近似,这使得控件由有限数量的参数参数化,之后优化),另一种同步方法(通过分段多项式近似状态和控制变量),最后提到了单一打靶方法与多次打靶方法(可能翻译得不准确,single shooting、multiple shooting)到这里就结束了关于动态优化理论知识的概述,但依旧很茫然,几种方法之间的关系,具体的分类依据都不是很清楚。
然后延伸着看了一下,结合下面几个回答,建立了一点认识。
如何通俗易懂地解释HJB方程? – 知乎 (zhihu.com)
关于最优控制问题求解方法的思考 – 知乎 (zhihu.com)
首先,最优控制的求解有三种主要方法:
- HJB方程/动态规划:都是基于最优性原理进行推导的,不同时刻做出的最优决策在未来时间都应该是一致的,然后HJB方程用于连续情况(看看如何理解HJB方程那个回答),动态规划用于离散的情况(看关于最优控制问题求解方法那个回答给出的例子)。
- 间接方法:也能称之为解析法,利用解析法求得最优值必要条件,再去迭代计算最优值,其中最主要的方法分支就是变分法。
- 直接方法:先将问题离散,离散之后将问题转化为非线性优化问题再进行求解,应该是用得最多的方法,至于其中的顺序方法与同步方法,我认为是在说离散程度,像有的文章中,分为部分离散方法与完全离散方法,部分离散方法只离散控制变量,然后在优化的时候,一步步计算每一个离散段,求解效率差,但完全离散方法同时将目标、状态、控制都离散,每一步迭代进行时,同步完成,但具体是啥意思还没看懂。
(优化工具背景)
本文将工具包分成了三大类:
- 模型集成性优化工具:一般将模型进行完全封装,方便不同软件间集成,但在优化过程中将模型视作黑箱模型,不会利用到其导数或者其他详细信息:modeFRONTIER、OptiY、ModelCenter
- 建模软件自开发优化工具:建模平台自身依据特点打造的优化工具,优点是使用教程较简单,但新算法的集成是一大问题。
- 以支撑动态优化的数据包为主的优化工具:使用多样的优化算法,但一般没有用户界面,并且对模型具有一定要求,需要自身对模型以及一部分优化工作完成编码,使用难度较大。
(Jmodelica完成的事情)
这里就按我看完之后的感觉来说一下,整个优化过程中,需要:1)良好的描述优化问题;2)良好的编译方法;3)易于控制的算法设定。
良好的描述优化问题包括待优化变量描述、成本函数描述、约束条件描述以及构成动态约束的Modelica模型,整个工作可以分为两个部分,一个是动态系统的描述,另一个是动态优化问题描述。
动态系统的描述文章中并没有指定描述方法,而是指出:对于不同结构的模型来说,应当利用不同的优化算法,模型的结构差异极大的影响了算法的适用性,这也表明,如果确定使用的优化算法,那么模型在搭建过程中是有要求的(虽然正常研究逻辑是先确定模型结构,再确定优化方法,但由于优化算法开发的巨大压力,依照优化算法对模型进行简化是常用的方式),当然,Optimica也可以拓展其他算法,增强通用性。
优化问题的指定比较有特点,制定了若干类,规范化约束、优化变量、状态变量的声明适用方法,这里就不过多介绍。
编译方面,就是将原本的Modelica系统模型,加上优化描述模型一起进行编译,使用JstAdd进行编译,具体细节原理就不太需要了解。
并且为了保证优化算法能够从模型中获取信息(我认为这一部分以及编译方式的不同是Jmodelica的主要亮点),JModelica构建了JMI,提供接口API,并适合与优化数值算法结合,例如使用CppAD进行自动微分(自动微分相关知识可以看看:自动微分法 – Hexo (loopvoid.github.io),感觉写得还行),从解析的方式获取系统描述方程的雅可比矩阵等等。
最后再优化算法上,基于python实现,极大方便了用户使用。
(示例与结论)
用了一下,评价了一下,就不介绍了。
代表图片









评论
还没有任何评论,你来说两句吧!