每次校准冷机时总忘记过程是怎样的,都得回头再看看公式与论文,在此,对冷机模型开发与校准工作进行重新梳理,并进行适当改造,使得其校准工作更容易进行(从人的角度,技术创新的咱现在不会)。
关于 DOE-2 冷机模型改进开发与测试文章标题:Development and Testing of a Reformulated Regression-Based Electric Chiller Model(基于回归的电动冷水机组模型开发与测试)
这篇文章说了什么?
介绍了一种新型电动冷水机组模型的开发与测试,并且对另外三种目前被使用的电动冷水机组模型进行测试与评估,指出其模型局限性,新开发的模型相比之下,新开发的模型在冷凝器变流量运行以及冷机低负荷运行时能够更准确的描述其现象。
建模目标
对冷水机组描述目标进行梳理,有如下需求:
- 描述计算各种工况下功率大小(工况指代,不同冷负荷、不同蒸发器温度、不同冷凝器温度)
- 当蒸发器与冷凝器流量变化时,及时做出响应
- 易于校准,使用易于获取的运行数据进行校准
- 易于建模,方程简单容易实现
- 适用于广泛的设备配置(风冷或者水冷、压缩机形式、节流阀形式)
- 对低速运行的离心机进行适当描述(冷凝器泄压)
方法论
- 对现有模型进行测试评估
- 选择DOE-2冷水机组作为基础模型
- 改进DOE-2模型,从而响应冷凝器水流量变化
- 改进DOE-2模型,使得其可以描述低负载下冷机运行情况
- 完善配套校准规范
现有模型测试与评估
在这一部分中,对比了三种模型,一种是DOE-2模型(源于DOE-2计划),一种是PT模型(ASHRAE工具箱中),还有一种是GNg模型(源于ASHRAE研究项目827),其中,将DOE-2冷机还按照使用的校准技术不同细分为两种(具体而言,是在对冷机性能曲线中第三条曲线——EIRFPLR进行校准时,A模型仅使用部分负荷率下的数据完成校准,B模型使用组合的全负荷数据与部分负荷数据进行校准),如下图所示:
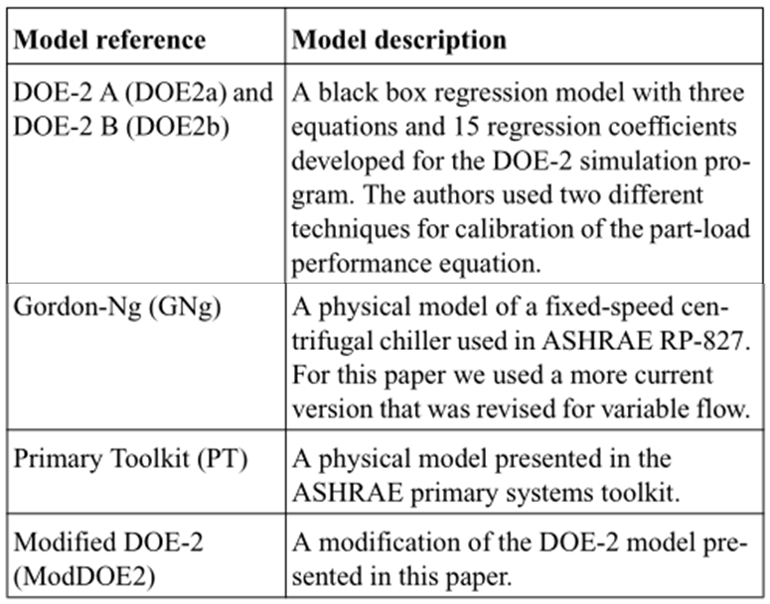
这篇文章测试的模型并不全面,BLAST、Trace、HAP、Energyplus中涉及到的冷机模型并不包含在内。
学者对模型测试评估,发现几个模型的局限性:
- DOE-2模型:在冷凝器水流量发生变化时,并不能相应的做出变化,并且在负荷率较低时,离心式冷水机组的功率存在较大的误差。
- GNg模型:对于定速离心式冷机描述较为准确,但对于其他压缩机并不能准确描述,明确不适用于变速驱动、非离心式压缩机、风冷冷凝器,但是其模型为物理模型,并非数据拟合获得,其参数具有诊断意义,其模型校准难度最低
- PT模型:校准难度极大,很难通过现成数据进行校准,其模型不适用于变速驱动,可以用于不同压缩机与风冷冷凝器,但不同压缩机或者不同冷凝器需要不同的模型格式。
模型的改进
Hydeman 和 Gillespie 在2002年试图对DOE-2模型进行修改,在部分负荷修正曲线中,添加冷凝器出口温度,来解决面对冷凝器流量改变对仿真结果无效的情况。
这里,先介绍一下,DOE-2模型的三条曲线
- CAPFT曲线:描述可用满载容量与两器温度之间的关系(这里是指满载制冷量,不是功率,使用的是 实际满载制冷量)
- EIRFT曲线:描述冷机满载效率与两器温度之间的关系(这里使用的是COP倒数的计算,并不是指代COP,并且,这里的COP是真正意义上的COP,是当前工况下满载制冷量除以满载电功率)
- EIRFPLR曲线:部分负载效率与负载率之间的关系(理解就是负载率对冷机功率的影响,如果是1表示任意负载率下冷机功率不变)
需要更新的一个认知是,前两条曲线,虽然大家在介绍时,容易说成是冷机的修正曲线,最开始只是一个描述曲线,描述的就是制冷量与COP两个东西,并不是修正,之所以后期看起来像 0.8 或者 1.2 这种修正量,那是因为整个曲线进行了归一化处理(被认为是一种较好的处理方法),然后一般而言,会将名义工况选做参考点,从而使得其看起来像修正系数一样。
用数学公式表述一下,以自己的认识写的,不太严谨,首先对前两条曲线进行定义,其中 CAP 开头意思是满载的意思,P是电功率,Q是制冷量,下标中ref是指参考工况点:
![]()
![Rendered by QuickLaTeX.com \[ EIRFT=\frac{\frac{1}{CapCOP}}{\frac{1}{CapCOP_{ref}}}=\frac{\frac{CapP}{CapQ}}{\frac{CapP_{ref}}{CapQ_{ref}}}=\frac{CapP}{CapP_{ref}\times{\frac{CapQ}{CapQ_{ref}}}}=\frac{CapP}{CapP_{ref}\times {CAPFT}} \]](https://yechuang.xyz/wp-content/ql-cache/quicklatex.com-f211f1a15a90faff66ca09dc7089b904_l3.png)
最后是第三条曲线的编写
![]()
定义完三条曲线之后,便可以计算得到冷机的实际负荷
![]()
模型规范化校准流程
从上文中对三条曲线含义的解释,可以对其校准过程进行规范化,以下过程首先解释DOE-2模型校准过程
首先,应当利用满载下运行数据对冷机模型前两条曲线进行拟合(此处之前我喜欢叫做校准,但结合原理,称为拟合更加合适)。
需要的数据有:
- 冷机蒸发器出口温度(满载工况)
- 冷机满载制冷量(满载工况)
- 冷机冷凝器进口温度(满载工况)
- 冷机满载电功率(满载工况)
其中,在实际操作中,会存在几个问题:
- 如果冷机满载制冷量没有直接监控量,使用冷机蒸发器进出口温度与流量进行转化计算。
- 实际数据很少有满载数据,因为加减载的存在,一般而言,可以利用电流百分比大于95%这样的指标来判定是否满载(当然,95%这样的指标都是自己定的,能够校准就行,自己改改)
![]()
![]()
完成满载性能的描述之后,利用前两条曲线,再加上一些新的数据样本点对最后一条曲线进行拟合,也就是考虑部分负载率对电功率的影响。
需要补充的数据有:冷机蒸发器出口温度(部分负载工况)、冷机满载制冷量(部分负载工况)、冷机冷凝器进口温度(部分负载工况)、冷机电功率(部分工况)
首先要计算部分负载率。负载率的定义是,当前制冷量占其最大制冷能力的比例,因此,用数学公式表达就是:
![]()
计算得到后,就可以进行拟合计算,拟合公式为:
![]()
以上是对传统DOE-2冷机的拟合,
改进
传统描述曲线有一个比较离谱的点,就是冷凝器侧使用的是进口温度,但不太适合(与之对应的蒸发器使用的就是出口温度,从原理上来说,出口温度更能代表两器温度,更加合理),当进口温度不变,但流量变化时,通常冷机功率是会发生变化的,因此改为冷凝器出口温度拟合,其几个公式变为:
![]()
![]()
![]()
其中,前两个曲线的修改合情合理,最后一条曲线在我看来,其修改并没有展现出奇妙之处,增加了项数在我看来,一定会让准确性提高一些。
这样一来,在模型校准时,就不再是需要冷凝器进口温度,需要冷凝器出口温度,如果没有,可以通过电功率、冷凝器进口温度、冷凝器流量、蒸发器进出口温度+流量(制冷量)来换算。
结果的对比
利用不同形式冷机(定速/变速),不同数据来源(全数据/现场测量)对各个模型进行验证,结果的分析就不说了,就是些数字的解释,结果如下:
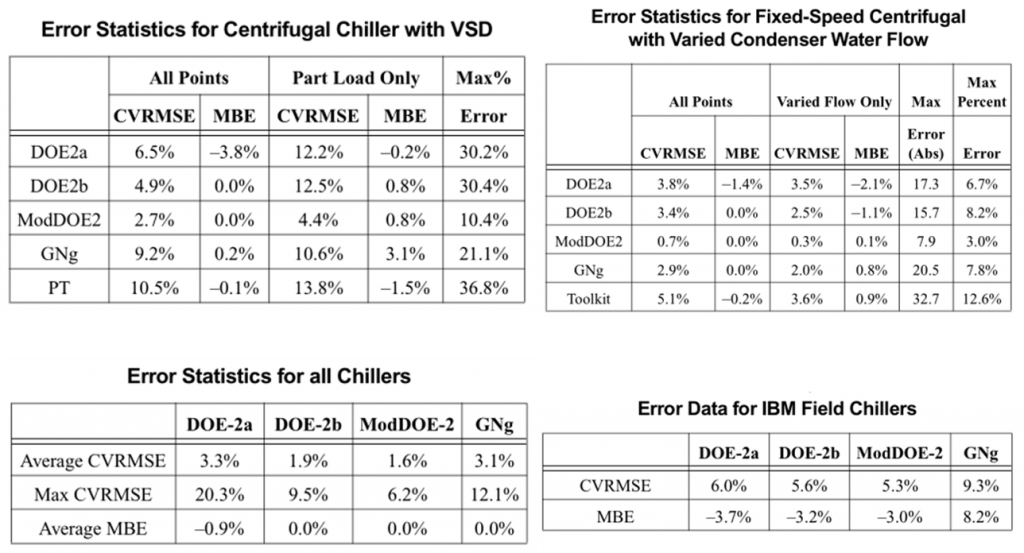
结论
结论无外乎,改进后的模型很棒,但也提到了几个点:
- DOE-2模型并非一个完全的物理模型,因此当样本点处于校准区域外时,模型将输出不可预知的结果,因此,建议使用参考曲线的校准方法,就是利用参考点(一般选择额定工况数据)对Capft等几条曲线进行归一化处理,这样即使不准也不会过于离谱。
- 通过现场测试数据来看,模型之间微小的差异会给整体能耗带来巨大影响,需要解决。
这种校准存在怎样的问题
问题主要来源于,这个模型并不是很机理,导致拟合得到的参数不具备物理意义,对其值的估计较难,如果利用基于优化的方法,难以得到初值以及寻优范围。
以第一条曲线为例,性能曲线各个系数0.01的差别都会对最后的结果带来较大差别。
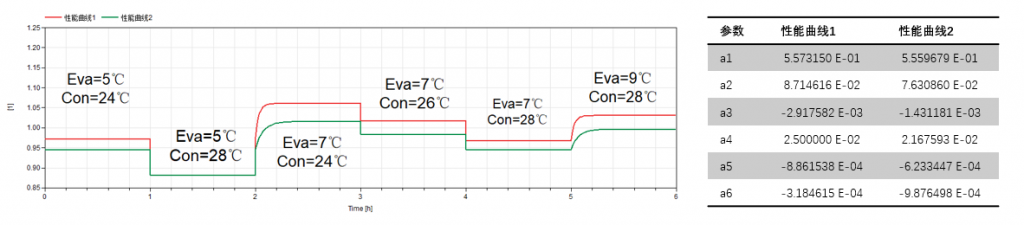
并且,当将39台冷机的系数进行汇总,试图找出各个系数的分布规律时,出现较大问题,各个系数分布并没有合理规律,如下图所示:

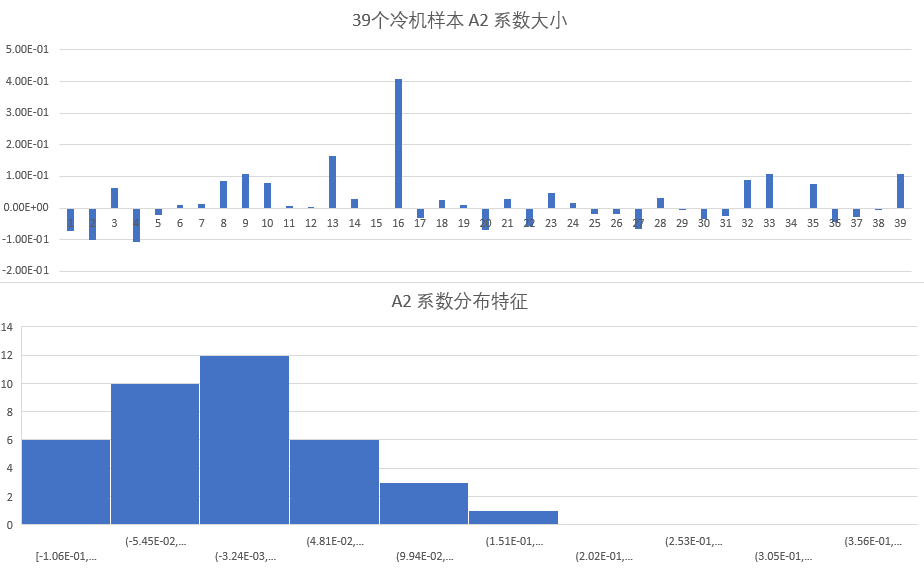
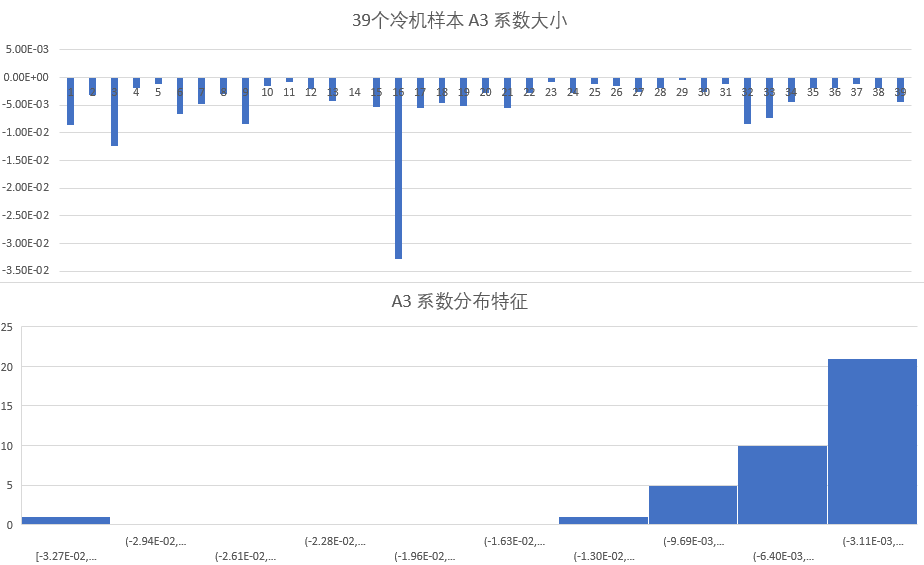
各个参数的分布由于参数本身没有物理含义,所以没办法建立先验估计,我认为,基于原有的模型,进行基于优化的迭代校准方法是很难的,即便能够实现,其迭代效率也是低下的,只有基于最小二乘的方法进行拟合才较为合适。
试图进行一点点改进
由于这次校准相关工作需要对比全局校准与分布校准,最好在校准方法上统一,以免降低结论的说服力,因此,我对模型进行了改造。
将原本需要自行计算得到的系数输入改为工况点输入,也就是将曲线拟合的工作放入到模型计算中,如下图所示:

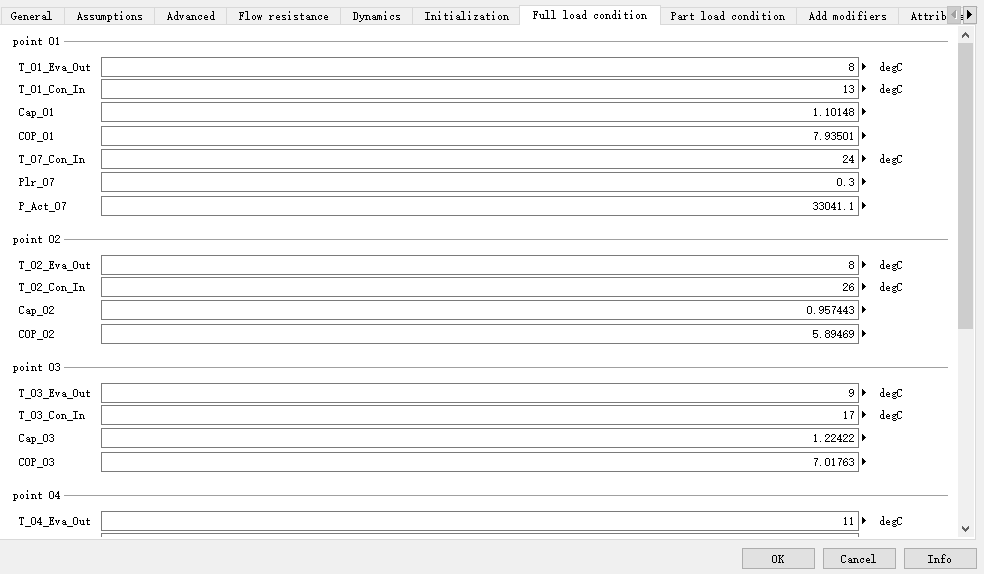
这样做的好处是,所有的参数都是由物理含义的参数,从而更直观,从而也可以来进行全局校准。
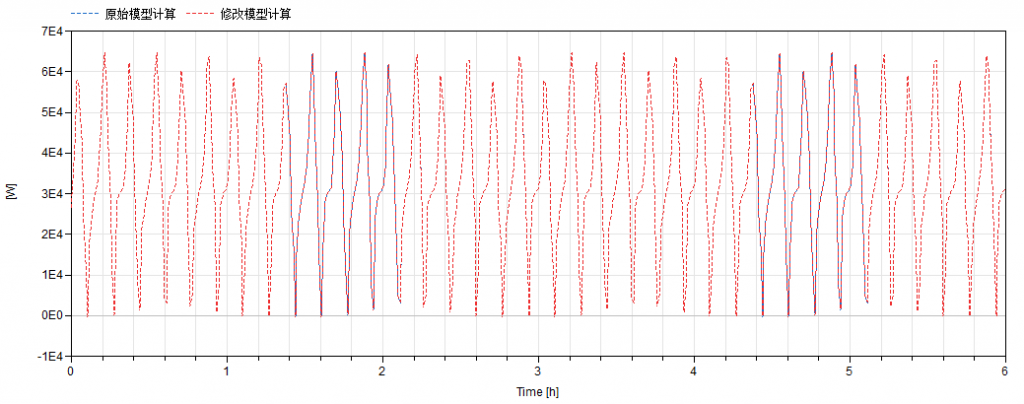
对比模型计算结果,可以发现效果一致。
关于实现过程,涉及如何利用modelica求解线性方程组的问题,虽然说这件事情在modelica中处理较为简单,但是其中一些现象是需要注意的,之后再开一篇文章进行说明。









评论
还没有任何评论,你来说两句吧!