在对北京丰台站进行优化时,当时我只会使用Genopt软件(可能叫做脚本更加合适)进行优化,所以没有在优化原理上花费过多精力,然而在描述完整优化框架逻辑时,感受到了莫大打击,还是得好好看看优化工具以及背后的优化方法,在看的同时记录一下。
这里主要阅读的材料是两个材料,一个是 Charles Audet 与 Warren Hare 一起编写的 Derivative-Free and Blackbox Optimization 这本书,很详细的讲述了为什么要使用黑箱模型优化以及怎样进行优化,角度偏向数学一些,但结合了工程案例,对其有效性以及收敛性都做了很详细的分析;另外一本是 Genopt 用户手册,当然,在用户手册中也介绍了一些方法以及收敛性,但比较简洁,可能看一下有点难以理解(例如本菜鸡就没看懂)。这篇文章讲主要以 Genopt 中的优化算法为依托讲述一下其中的优化算法。
[PDF]无导数和黑盒优化 (semanticscholar.org)
为什么我们要使用面向黑箱模型的优化方法
在介绍原因前,先区分一个概念,需要注意的是,这里的黑箱模型并不是说模型在构建时是采用黑箱建模的思想,而是说在优化过程中,仅仅只使用模型的输出,对模型结构以及模型信息没有任何要求,即使建模时使用的是基于白箱的模型,也可以利用面向黑箱模型的优化方法。
综合书上所说的以及这两年自己的感受,总结了以下采用面向黑箱模型的优化方法的原因:
- 模型构建的问题:模型的特点让人不得不使用面向黑箱模型的方法,工程中经常会出现所构建的模型不支持常用优化方法的问题,在这里面有两个容易触碰的场景
- 第一个是“遗留模型的问题”,在很多工程项目中,常常会出现软件技术更新换代的情况,一些早期构建的模型由于维护成本的问题,难以进行改造或者重建,使用只能作为黑箱模型使用(只能获取输入-输出对应序列);
- 第二个场景是“模型集成的问题”,目前,由于计算机程序的发展,越来越多的领域开始借助计算机来辅助各种研究,而建模技术的发展,在方便建模人员使用的同时,又在另一方面将模型层层包裹,集成化的建模思想让建模人员难以在不借助外部工具的帮助下获取模型的更多信息,例如 modelica 语言,其本身高级的语言特点使得模型的构建变得容易但模型数值相关的分析变得复杂,再加上 Building 库的创建让模型信息被层层包裹,虽然让大家只需要拖拖模块就能完成模型的构建、展开选项卡就能够集成求解算法,但如果想要获取模型的梯度或者伴随矩阵,就变得很艰难,虽然 Jmodelica 项目试图帮助大家解决这一问题,但从现状来看,距离使用还是有一段距离。
- 优化约束的问题:实际工程中,优化变量的约束是多种多样的,而很多约束是预先难以知道的,一些变量在越过约束后甚至会出现模型报错的情况,此外,很多优化约束并不是以数值作为边界,也只会以“是”或者“否”的方式描述是否可行,这时候一些基于黑箱模型优化的方法可以协助这种问题的解决。
- 信任度的问题:利用黑箱模型进行优化,其速度虽然感人,但由于其优化过程更符合人的思维(很多启发式算法,例如遗传算法或者粒子群算法,可以用大家容易理解的方式讲述),并且,其虽然可能陷入局部最优,也有可能最终迭代不收敛,但是并不妨碍其更优的特点,并且由于其已经在模型中执行了一边,工程人员也会对其产生信任。
利用面向黑箱模型的优化方法进行优化有什么缺点
在我看来,缺点主要有两个,一个是慢,一个是近似最优,最后一个是普适性。
首先对慢这个缺点进行说明:由于黑箱模型内部信息不可知,面向黑箱模型的优化方法其实都是利用模型计算结果去猜更优的设定值在哪里,例如 这种问题,利用黑箱模型去解决时,其解决思路类似于先计算出 ; 以及 ;,然后猜测 时效果会更好, 这种方式需要反复迭代获取模型特性,并且模型的计算速度是很慢的,基于迭代的方法需要消耗大量的计算资源,但如果优化方法能够i获取梯度,那么模型将直接知道,从而知道时,函数将达到最小值,这时候就不依赖于模型的大批量计算,计算速度也会得到提高。
这其实就是一个权衡,是忍受缓慢的优化迭代过程,还是在优化前赋予模型更多的功能,使得其计算结果能包含更多的信息,但是目前来看,面对建筑能源系统,忍受缓慢的迭代计算过程更容易接受,建筑能源系统本身的复杂机理导致模型的任何改进都需要大量的专业知识与技能,在另一方面,建筑能源系统控制的主体还是热,热的动态是较慢的,其控制也不必需要那么快的速度,因此,前者是现阶段最合适的方法。
再来说一下近似最优这个问题,这个词是我猜的,想表达的主要是面向黑箱模型的优化方法一般收敛性都是有限的,黑箱模型本身形态不一样,不能够像传统优化方法那样获取准确的最优性条件,依靠猜的方法去得到最优解很难让人看到完整的模型全貌,其体现就是,无论是在优化执行前,甚至是优化结果获取后,优化人员都很难说优化是不是达到了最优或者说是迭代成功,例如利用遗传算法去执行优化时,谁能完全保证出现了正好的突变获取到了最优的结果呢?但在另外一方面,建筑能源系统的优化主要还是经济性优化,达到最优经济性固然最好,但相较于现状实现更优也不是不能接受,工程永远不需要像数学定理一样绝对性的证明一件事,提高现状就是成功。
最后说一下普适性这样问题,个人认为面向黑箱的优化方法永远是一个个性化的方法,因为面向的是黑箱模型,很难提出对于模型的要求,面向一个项目调整参数获取到的优化参数不一定适用于其他项目,如果试图构建完善的建筑能源系统在线优化控制框架,还是应当尽量尝试获取模型更多信息,包括梯度,然后从模型固有的特点出发提出优化方法。但这一点需要声明,我也是不确定的,它似乎是一个问题,但面对能源系统它似乎可能并不存在,黑箱,就是不确定。
面向黑箱模型,充满了不确定性,似乎是条捷径,但似乎又是一条歪脖子树。
如何利用黑箱模型进行优化
在进行介绍时,主要利用 Derivative-Free and Blackbook Optimization 这本书,但在对具体方法进行讲述的时候,编写一个个方法来讲述太过艰难,主要还是我菜,因此主要以 Genopt 软件中已经完成的优化算法进行展示。
整体概况
首先,首先提到两个概念,就像书名所说,Derivative-Free and Blackbook Optimization,里面会涉及DFO(无导数优化方法)以及BBO(黑箱模型优化方法),从我直观的方式来看,这两个名字并没有太大关系,一个是说计算过程中不依赖导数,另一个是说解决的问题是面向黑箱模型的,所以我不希望把两者分离开看待。但从书中所给出的定义来看,DFO 被定义为:Derivative-free optimization (DFO) is the mathematical study of optimization algorithms that do not use derivatives,而BBO被定义为:Blackbox optimization (BBO) is the study of design and analysis of algorithms that assume the objective and/or constraint functions are given by blackboxes,他们两者之间的区别在于:
- DFO的研究对象不限制于黑箱模型,只是不使用梯度,当面对一个优化问题,该优化问题可以计算梯度但计算难度较大时,应当利用DFO进行研究,因为它相对黑箱模型能够提供一些信息,至少其目标函数的性质能够有一定了解。
- DFO更偏向于数学研究,对于算法收敛性的要求高于BBO,基于DFO算法的框架普遍拥有强于BBO的算法。
这里用一个列表来表明这类问题解决方法的大致情况:
- DFO(无导数优化方法)
- 直接搜索的方法:计算函数值,基于函数值进行迭代操作,不对导数进行近似(例如 坐标搜索、遍历搜索)
- 基于模型的方法:利用部分点的函数计算结果,假设目标函数的形式,从而指导最优点的得出(例如一阶下降方法、信任域的方法)
- BBO(黑箱模型优化方法)
- 启发式算法:利用一些有意思的规则来指导迭代工作的进行(例如 遗传算法、粒子群算法、单纯形N-M法)
- 代理模型的方法:基于输入-输出关系,生成代理模型,降低模型计算成本。
- 混合优化方法:结合不同方法进行优化,例如GPS算法中可以使用粒子群进行全局搜索,之后进行坐标搜索,综合使用各部分优化算法的好处。
具体方法介绍
从这一部分开始,主要参考 Genopt 中的实现过程,在这本手册中,前面几部分对建筑能源系统为何使用这种面向黑箱模型的优化方法进行了解释,其中有一点很关键,建筑能源系统模型包含了模型描述与求解器,也就是说除模型本身的非线性特性以及离散特性导致系统难以使用传统优化方式外,求解器的数值误差也是一大影响因素。手册的后面的部分就是介绍优化算法以及其使用,这里从第五章说起:
GPS(Generalized Pattern Search Methods)
暂时先翻译为“广义模式搜索算法”,GPS算法是在原有的CS算法上改进发明的,其发展可以说:最开始是基于遍历的算法(ES Exhaustive Search),就是简单的生成大量的样本点,然后计算,找到最小的那一个,然后这种方法点太多,如何生成是一大问题,于是产生了网格遍历的方法(GS Grid Search),就是在变量可能取值的区间进行网格划分,同样,当优化变量维数提高后,大量的点计算成本过高,后出现了坐标搜索的方法(CS Coordinate Search),就是找到一个点之后,只在它周围找点,发现更小的点就往其位置移动,但依旧存在两个问题,一个是移动步长有限,最优值难以精确,第二个是容易陷入局部最优,于是产生了GPS算法。
GPS的主要计算分为两个部分:
第一个部分较广的选择候选网格点(search step),也就是名字中的 pattern 部分,pattern move,可以理解为基点的移动,这种移动方式是开放的,并没有限制具体方法,就像整体定义中 “ for some in a finite subset of the mesh ”,只要是网格中的有限点位即可,就像是更大的范围内去找点,如果找到了就更换,没找到就呆在原地,基点不动。例如在 Hooke-Jeeves 方法中,以上一个点的计算结果与得到的新的更优点为依托,延申得到新的搜索点。
第二过程是循环查找(poll step),探索步,Exploratory move ,也就是在确定好的基点中进行寻找,这种寻找是没有任何依据的寻找,不像 pattern 一样具有一定的搜索方向,一般选择坐标轴方向为搜索方向,就像CS一样在周边寻找最小点。
两个过程循环进行,不断改变步长寻找,用下面这张图来说明,下面这张图来源于无导数方法在受限的石油生产优化问题中的应用,使用的是 Hooke-Jeeves 的方法进行 pattern move。
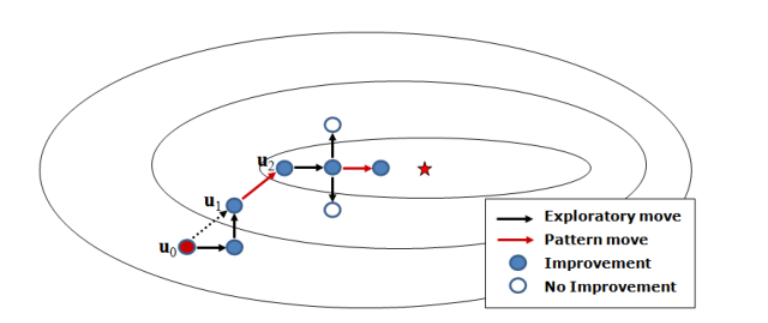
相较于单纯的CS方法,GPS有3点不同:
- GPS允许更多样的搜索方向,而CS只指代正负方向;
- GPS拥有变步长机制,计算结果更优;
- GPS拥有search step,可以在一定程度上避免局部最优。
因此,从上述描述中,GPS的执行有两个关键点,一个是如何构造搜索网格,进行 Pattern move,另一个是如何进行细致的搜索,也就是Exploratory move。
原理的逻辑清楚后再来看看具体的实现过程,这里以Genopt为例进行解释。
在 Genopt 中,搜索方向已经被指定,采用沿坐标轴的方式,此外,采用最大正基的方式生成方向(也就是说当删除 search step 时,除了变步长机制,GPS也是想CS一样沿着坐标轴进行寻找,GPS 与 CS 没有任何区别,因此 Genopt 中,Coordinate Search Algorithm 在介绍是使用的依旧是 GPS 框架)
剩下的东西具体没太看懂,主要就是说,要依次进行两种搜索,然后介绍了以下两个搜索集的制定方法,global 与 local,对于上方应该是 search step 与 poll step ,说明手册中的叙述方法多少带点误导信息,没有按照区分两个搜索集的思路去写,虽然显得很有逻辑,在论述 Hooke-Jeeves 的执行方法时,特地写了一个 Global Search Set Map,但里面却又包含了 Local Search Set Map,当然后面也解释了这一点,但是我还是想吐槽。
幸好有一个实现方法解释:
Local Search Set Map 设置方法

Hooke-Jeeves Global Search Set Map 设置方法

此外,GPS算法也可以多起点同时进行,通过将 MultiStart 关键字赋予 Uniform 即可,在运行时,将依照给出的优化变量范围,均匀选取初始计算点(数量是自定义的)。
| Main | GPSCoordinateSearch | 坐标搜索算法(适合于连续变量的优化问题)(个人认为不叫GPS) |
|---|---|---|
| MeshSizeDivider | Integer | 用于搜索系数,制定第k阶段搜索步长,通常取2 |
| InitialMeshSizeExponent | Integer | 用于搜索系数,制定第一步搜索步长,通常取0 |
| MeshSizeExponentIncrement | Integer | 害,自己看吧,没公式不好解释 |
| NumberOfStepReduction | Integer | 害,自己看吧,没公式不好解释 |
离散Armijo 梯度
这种算法是通过有限差分的方法来逼进梯度,从而支撑优化进程,因此,希望目标函数是连续可微的,也就是前文中说到的解决的是,梯度是存在的只是获取难度大的问题,个人认为在本领域由于大量离散过程的存在,这种算法很难获取较好的效果。(在使用文档中也说到,离散Armijo算法对目标函数中的不连续相当敏感,对于需要数值积分求解的模型是一种较大的打击,不推荐Energyplus这样的软件使用这样的方法)。
算法的过程也比较简单,计算梯度,移动梯度,依照梯度进行精确线搜索…….这里就不详细说明。
粒子群优化算法
粒子群算法,全称:Particle Swarm Optimization,模拟自然界鸟群捕食的过程,通过群体中信息交互与协作寻找问题的全局最优解,在处理不连续优化问题时具有较好的优势。
其实现起来方法原理还是比较简单的,简单点说就是当一个群体中一个粒子的移动将参考粒子自身移动的历史记录以及周围领域粒子的信息。
用公式表达就是:
其中 以及 表示两个 0~1 之间随机数, 表示第i个粒子,在之前所有代中产生最优值的位置, 表示前面所有代中产生的最优值的位置, 表示粒子当前移动对自身经验的依赖程度, 表示粒子当前移动对粒子群社会知识的依赖程度,因此,一个被叫做认知加速常数,另一个叫做社会加速常数。
但这时候,会思考到一个问题,如果过多的考虑的其他点,是否会使得整个优化陷入局部最优,简单说,就是每次都以全局最优的为标靶,就还是会慢慢被某一个碰巧达到局部最优的点所影响,如何均衡全局与局部,也是研究的一大热点,其中邻域拓扑结构的研究就是一大重点。
在 Genopt 中提到了三种领域:
- lbest:中文应该叫局部邻域,粒子在参考点前后相邻点进行信息传递,好处是局部与局部会被很好的区分开,整个模型不容易陷入局部最优解,但缺点是点在迭代时获取到的信息有限,收敛速度一般较慢。
- gbest:中文对应应该是全局邻域,也就是讲种群中所有的点,在这种模式中,信息的传递是很快的,但缺点是容易陷入局部极小值点。
- von-Neuman:冯诺依曼邻域,最简单画一个四方网络,每一个粒子与其上下左右邻近粒子相连,形成一种网状结构。有的网站中介绍到,von-Neuman结构在lbest与gbest结构中取得了一个较好的平衡,适合于大多数的问题求解,并且都具有较好的性能。这里需要注意的是,Genopt使用二维晶格,在使用von-Neuman结构时,因为使用的是上下左右这种,就会出现边界的问题,于是Genopt中做法是构造正方形晶格(因此,粒子群粒子数量得取平方次,4、9、16这种数,如果不存在,那么就比其大能够开方的数字),然后收尾相连构成完整闭合面,如下图所示。
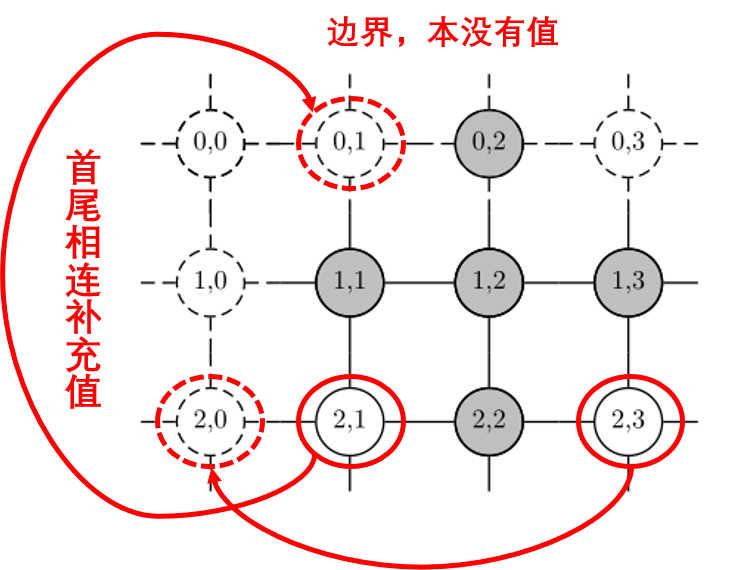
将上述过程进行整理,其大致算法实现如下:

以上便是传统 PSO 算法,后来,很多人对粒子群算法的粒子迭代计算方式进行了修改,形成了以下几个方法:
PSO with Inertia Weight(for continuous Variables)
计算每一个点移动速度时,原有计算方法是这样的:
那么对它进行适当改造,比如在其直接继承上一阶段速度这一点进行修改,考虑到越靠近最优点速度正常会出现下降,因此给速度加上一个权重,如下所示:
其中,,建议 取值 1.2, 取值 0。
最后加上对速度的限制,防止粒子群跑出界限,公式就不打了。
PSO with Constriction Coefficient(for continuous Variables)
在原有公式的基础上,对移动速度进行限制,不仅仅是限制前一个速度,是对整体进行限制:
其中就是搜索系数,其包含一个计算公式,由来控制收缩程度,例如当取值1时,就不进行收缩,收敛很慢,具体取值有很多方法可以参考,不进行介绍。
以上就能完全实现面向连续问题的PSO解决方法,接下来加上离散问题的处理方法。
PSO for Discrete Variables
面向离散问题使用上述连续问题时,涉及到一个问题,每一个得到的都将是一个连续的值,这对离散变量下一个点的寻找产生干扰。其实也没太大区别,原有实数是采用实数编码的方式,离散变量就采用二进制编码或者排列编码的方式。在Genopt中,使用Gray encoding的编码方式,将离散变量转化为二进制,然后利用粒子群算法对每一位(0,1)进行迭代更新。
这种改变导致迭代过程需要进行适当调整,对于连续变量(实数编码格式),原来的速度可以直接将方向与大小一同描述(实数有着连续的大小变化能力),但二进制编码的情况下,这个速度描述的内容需要进行改变,二进制只有0或者1,因此速度需要支撑像0转变还是向1转变,整个的过程如下:
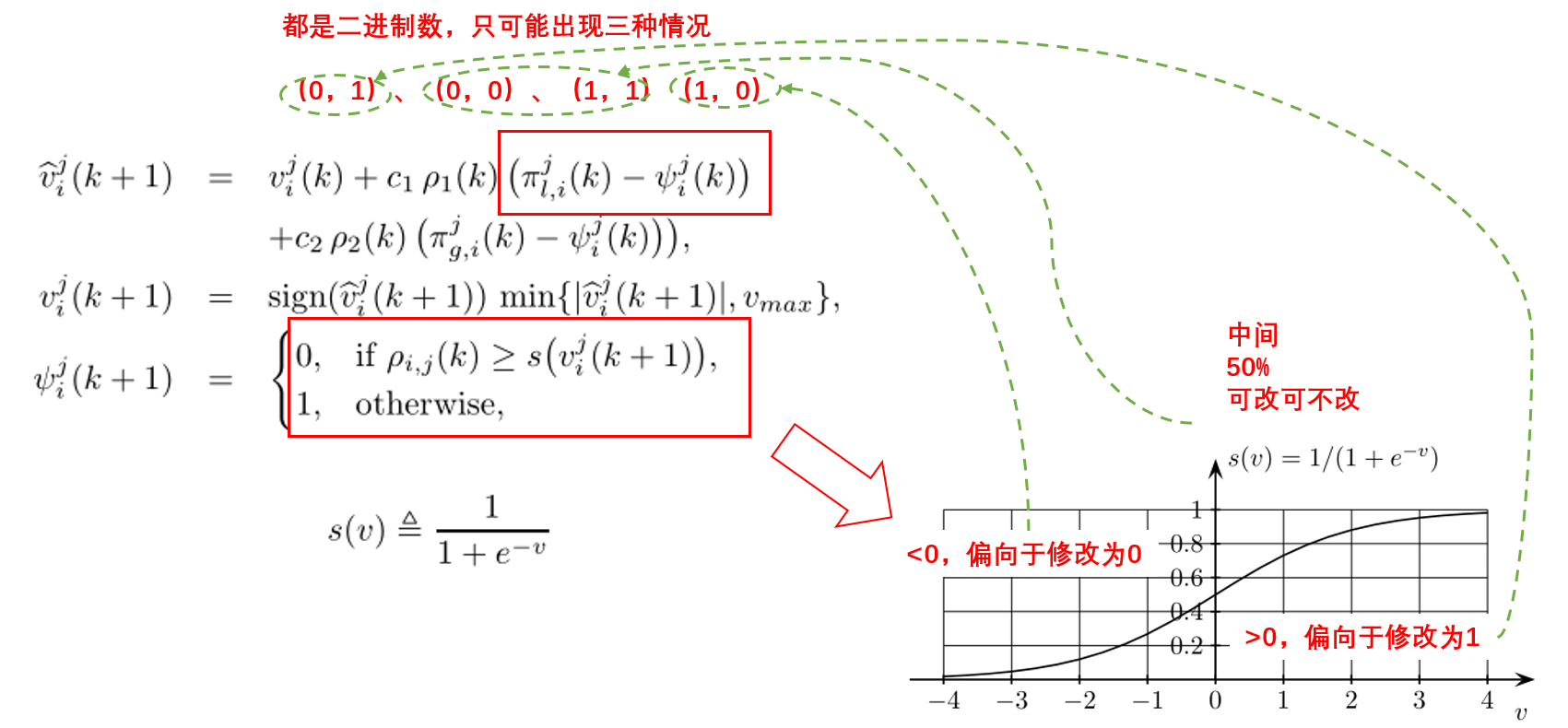
这里可以说一下我对Gray encoding的看法,不知道翻译得对不对,“格雷码转化”?从其他网站上介绍,这种编码格式的特点是两个相邻元素只会有一位元素不同,就是说,比如在2进制中,“0111”表示“7”,10进制中7的下一个是8,这是其2进制变为“1000”,4个位置上的元素全部都发生了变化,想象以下,当优化过程中,明明快达到最优点,而因为二进制的问题,需要将所有元素进行修改,这种情况我猜会导致反复迭代的产生,而格雷码不同,7的格雷码为“0100”,而8的格雷码是“1100”,只改变1位,这种可能对优化有好的帮助。
PSO for Continuous and Discrete Variables
从上述算法过程中可以看出,这些算法可以放在一起使用,都是在一个框架下的,因此,遇到混合问题,直接将连续变量与离散变量分别处理就行了。
PSO On a Mesh
从个人角度来看,这种方法应该是为了降低一些性价比很低的搜索,提高迭代获取最优值的速度,正常来说迭代最后会在某一处一直计算,连续变量不断改变逼近最优点,但这种过程性价比过低,因此可以根据需要的精度,将连续变量离散成为网格,当在某一个网格内,系统将自动计算网格点处输出并返回,这样就降低计算成本。
| Main | PSOCCMesh | 网格化的粒子群算法(适合于既含有离散变量又含有连续变量的优化问题) |
|---|---|---|
| NeighborhoodTopology | gbest/lbest/vonNeumann | 邻域拓扑方案,一般使用vonNeumann,比较适中 |
| NeighborhoodSize | Integer | 领域拓扑数量,只对lbest领域拓扑方式有效,其他形式该关键字会被无视 |
| NumberOfParticle | Integer | 一代中粒子数量 |
| NumberOfGeneration | Integer | 粒子群迭代次数 |
| Seed | Integer | 用于初始化随机数生成器,在介绍文档中,并没有关于其解释 |
| CognitiveAcceleration | Double | 个体系数,有多依赖个体前期经验 |
| SocialAcceleration | Double | 社会系数,有多依赖社会前期经验 |
| MaxVelocityGainContinuous | Double | 用于限制粒子移动速度,如果设置为0或者负值,将不受速度控制(对连续变量) |
| MaxVelocityDiscrete | Double | 用于限制粒子移动速度,如果设置为0或者负值,将不受速度控制(对离散变量) |
| ConstrictionGain | Double | 没用,对PSOCC用的 |
| MeshSizeDivider | Integer | 网格划分时用到,>1,越大网格越小?不确定 |
| InitialMeshSizeExponent | Integer | 和上面那个参数配套用的,会出现啥也不清楚 |
拓展N-M单纯形法
很神奇的名字,也叫单纯形法,但是并不是线性规划中的那个单纯形法,因此为了避免错误,很多就直接叫N-M方法,一般用于解决连续优化问题或者连续待约束优化问题,但需要注意的是,它优化时,优化变量的数量必须大于1。这种方法在最终的收敛性上表现很差,甚至无法收敛到一个平稳点,但对于实际工程项目来说,尤其是当优化变量维度较高时,它总能发挥作用。
先对它的大概原理做一个介绍,这个是我自己的理解,可能不对,在一个N维空间中,要想通过几个点之间的信息推测更优点,就需要N+1个点,然后通过移动表现最差的来获取更新的点(更换的方式有三种主要操作:反射、收缩、展开),如下图所示:
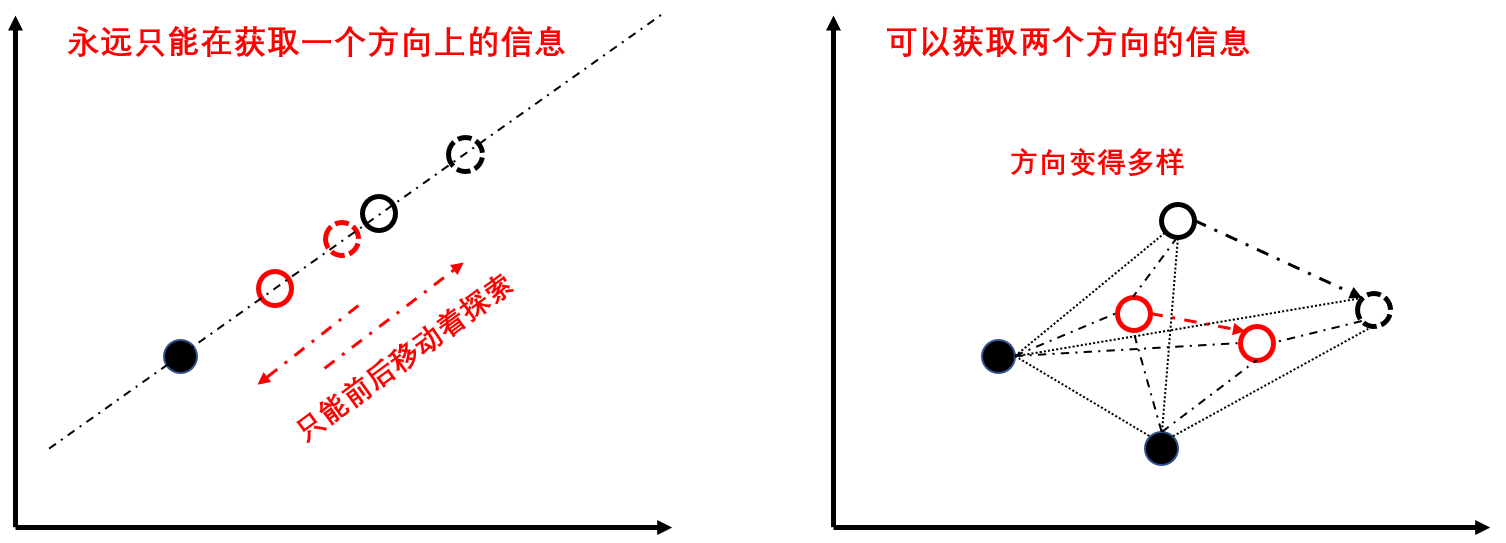
对三种主要操作进行解释,直接用图说就行,其中的、、 这些对应的就是是吗收缩系数、反射系数、展开系数等等。
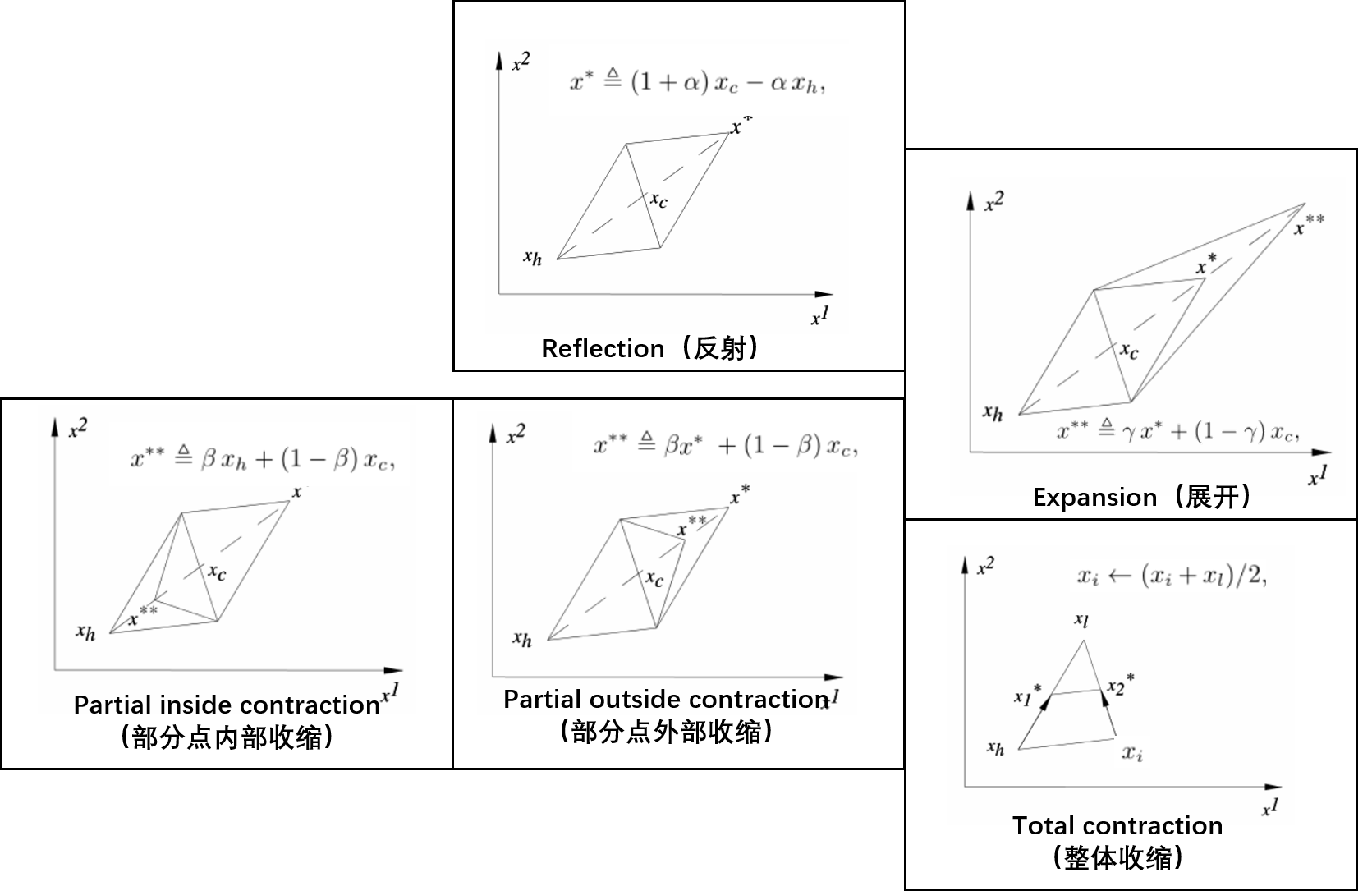
之后说一下N-M主算法的执行流程:
- 初始化,生成N+1初始单纯形,
- 计算,得到其对应的函数值并排序
- 进行反射环节,将最差点进行反射,计算反射之后的值,会产生三种情况
- 出现相比原有最优值更优值,说明最优点在外部,那么尝试向外拓展,展开侯结果有两种
- 展开结果形成最优,利用 代替 ,并转回步骤2
- 展开结果未形成最优,利用 替代 ,并转回步骤2
- 没有出现比原有最优值更优值,并且,除去原有最优点,新产生的并不是最差的点,那么认为还可以继续反射,暂时不用收缩,转入步骤2
- 没有出现比原有最优值更优值,并且,除去原有最优点,新产生的是最差的点,那么开始收缩,其中也有两种情况
- 新产生的比原有最差点还差,那么部分点内部收缩
- 新产生的比原有最差点好,那么部分点外部收缩
收缩完成后,进行判断,如果依旧是最差的点,那么再进行一次整体收缩,将得到的替代 ,转入步骤2
- 出现相比原有最优值更优值,说明最优点在外部,那么尝试向外拓展,展开侯结果有两种
- 终止条件,原有的N-M方法中的终止条件是依靠计算单纯形的方差来判断是否终止的,但这种方式在建筑能源系统中很难达到,很容易出现不收敛的情况,至于具体原因,还没有看懂它的解释,Genopt采用O’Neill的修正方法,在计算完一次后,计算下它前后方向是否不再回出现下降来判断是否达到最优,但这种方法使用还会存在问题,面对我们的系统,因为最终的结果容易出现阶段误差,所有很可能并没有输出去具体差别,因此又进行了很多改进,这里就不细说了。
GPS+PSO算法
可以用于求解连续优化问题或者带不等式约束的连续优化问题。其在运行时,首先运行粒子群算法,之后选择最优的粒子作为起点,进行GPS搜索,当存在离散变量时,在粒子群算法结束后,将固定离散变量的值。实现起来就是一个组合过程,没有什么特点。
这样一来,粒子群算法努力避免局部最优的出现,GPS确保最终收敛效果,双赢。
区间划分
区间划分的方法一般用于单个连续变量的优化问题,Genopt中实现了黄金分割法(Golden Section Interval Division)与斐波纳契分割法(Fibonacci Division)。
黄金分割法方法很简单,在很多场合都有使用,其实就是考虑如何划分可以提高效率,特别是曲线变化不均匀的时候,当抛弃两侧以及下一次计算结果所包含的比例一致时,就认为是效率最高的,,然后计算 就是黄金分割比。
斐波纳契分割法感觉就是一个黄金分割法与二分法的结合体,1、1、2、3、5、8、13……,到后面其实后一个数除以前一个数就是黄金分割比,只是用一个简单的数列的形式展示出来。









评论
还没有任何评论,你来说两句吧!