本篇文章将主要讲述Building库中冷水机组模型的计算机理,主要帮助理解冷机模型,使用校准在另外一篇文章中会提到。
概述
我们一般使用伯克利开发的Building库模型,目前Building库中冷机模型包括卡诺冷机(Buildings.Fluid.Chillers.Carnot_TEva、Buildings.Fluid.Chillers.Carnot_y)与DOE-2.1冷机(Buildings.Fluid.Chillers.ElectricEIR、Buildings.Fluid.Chillers.ElectricReformulatedEIR),此外,8.0库(也可能是7.0库)之后的库文件中增加了吸收式冷机(Buildings.Fluid.Chillers.AbsorptionIndirectSteam),其中,从文献来看,DOE-2.1 模型的使用频率是最高的,这主要得益于其不要求建模者对于模型机理有较强理解,利用几个修正系数直接跨过冷机运行机理对冷机进行建模。
基础知识
首先是对暖通空调领域常用的制冷循环机理进行了解,在空调用制冷技术中,实现人工制冷的方法有:
- 液体汽化法(常见的蒸汽压缩式制冷、吸收式制冷,都是借助制冷剂在低压中进行吸热然后在高压中进行放热两个过程实现制冷效果,不同的是一个是借助压缩机实现低压到高压的转变,另一个是借助溶液的吸收与发生过程实现低压到高压的转变)。
- 气体膨胀法(借助高压气体膨胀吸热来实现制冷,例子不太常见,之后有例子再进行补充。
- 热点法、固体绝热去磁法(都不太常见,也不是很了解)
蒸汽压缩式制冷热力学原理
介绍蒸汽式制冷循环离不开两个基本循环的介绍,一个是卡诺循环,另一个是劳伦兹循环,后者就是前者的一个小的变形,重点还是在于卡诺循环。对于卡诺循环,由四个过程组成等温膨胀(A→B)、绝热膨胀(B→C)、等温压缩(C→D)、绝热压缩(D→A)

为了便于理解,可以想象一个活塞式发动机的运行过程,其过程对应就是,活塞向里压缩,空气被压缩(C→D),然后是喷油嘴喷油,电火花打火(D→A)(注意:此处并不是绝热压缩过程,只是为了便于理解假想一下),之后活塞回退,启停膨胀(A→B),最终排气口打开,气体膨胀到大气压(B→C)。
画在T-S图中便很容易理解为何卡诺循环是两个温度源之间效率最高的循环:面积ABCD与面积DCFE之比(好像是这样吧,当时理解的就是,热机从一个热源吸热后,并不能将吸收的热量全部用于做工,因为低温热源会在路上抢劫一手,具体公式倒是不记得了,效率以及熵的计算都忘光了)

将卡诺循环反过来进行就是制冷循环,逆卡诺循环,先时等温吸热过程(D→C),从低温段吸收热量,然后等熵过程(C→B),将制冷剂绝热压缩,提高其压力,由于是绝热过程,因此其温度在这一过程中大幅升高,之后是等温放热过程,利用 CB 阶段创造的高温势差向高温热源放热,最后是一个绝热膨胀过程(A→D),放完热的介质绝热膨胀,压力降低,温度降低,得到低温介质,继续送入低温段吸收热量,周而复始。从运行过程中便能看出,制冷循环的关键就是创造压差,通过加压的方法使得介质在包含有“相同热量”的情况下得到更高的温度,从而可以向高温介质放热,通过降压的方法让介质温度降低实现从低温段吸收热量的目的。
在温熵图中,中间ABCD的面积就是制冷循环中压缩机做工,下面DFED便是从蒸发器中吸取得到的热量,最大的面积ABFE就是通过冷凝器释放的热量。
以上是理想的制冷循环过程,但是在实际的制冷循环中,有3个方面导致其与理想制冷循环有差距,因此需要进行修正。
- 利用了膨胀阀代替了膨胀机:理想情况下是使用膨胀机也就是从A点直接下降到D点,使用膨胀机其目的就是为了充分利用高压制冷剂变为低压制冷剂过程中膨胀的功,但对于液体制冷剂来说,膨胀功本就很小,再加上膨胀机的摩擦损耗,就显得得不偿失,因此利用膨胀阀代替膨胀机。其热力上的影响就是将原本的可逆绝热膨胀过程变成了不可逆的绝热节流过程,图中就是从 D‘ 点移动到 D’‘点(其大小的计算暂时不去考虑,之后将另写文章进行介绍)。
- 换热温差问题:在实际换热过程中,制冷剂在蒸发器侧的温度无法与低温侧介质温度完全一致,同理制冷剂在冷凝器侧的温度也无法与高温侧温度完全一致,因此相较于理想制冷循环,蒸发器侧温度会下移,冷凝器侧温度会上移。
- 干压缩的需要:在C到B过程中,理想制冷循环是在气液共存区工作的,液珠会给压缩机的运行带来较大伤害,一方面,液珠接触到温度较高的气缸壁会迅速汽化,占据气缸空间,使得制冷剂流量迅速下降降低制冷量,另一方面,液珠过多时,难以全部汽化,不仅会损伤压缩机气缸壁的润滑性,还会造成液击现象,导致压缩机损坏,因此采用的方法是保证压缩机处于干压缩状态,增加气液分离器,制冷循环图中,C’ 点也随之移动到C‘’ 点。
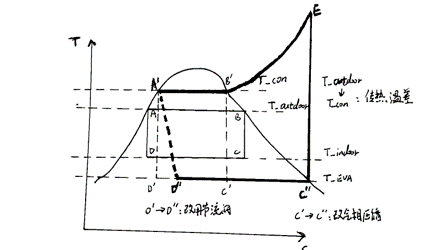
蒸汽压缩式制冷循环运行调节方法
上面对于循环的了解只是了解了一个工况下,制冷循环的流程方法,那么还需要了解其在运行过程中是怎样调节各部分运行实现出力负荷的变动,这部分的基础知识得从其各个部件展开说明。
制冷循环中有四大组件,压缩机、冷凝器、节流装置、蒸发器,每一部分对可以设置控制环节,下面将依次说一下其中的控制过程。
首先是压缩机,制冷压缩机的形式很多,容积式制冷压缩机(周期性吸入气体进行压缩)与离心式制冷压缩机(连续吸入气体进行压缩),由于常见机房使用的制冷压缩机规格较大,一般都是使用离心式压缩机,当然,螺杆式压缩机(属于容积式制冷压缩机)也常用于大型空调系统中,这里不去详细说明其区别,这次就介绍使用频率高的离心式压缩机。
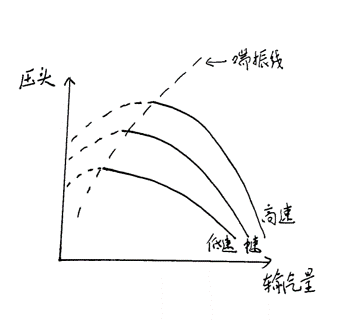
离心式压缩机其实就是一个泵,其性能曲线就是泵的性能曲线,如下图所示,其调节方法我认为就两种,一种是调节转速(压缩机转速),另一种是调节旁通量(直接将压缩机部分出口制冷剂介质引入到压缩机进口,因此压缩机整体流量保持大致不变,而蒸发器冷凝器的流量减小),前者适合与较高负荷下的调整,低负荷时会出现喘振现象,后者可以有效的防止喘振现象,但是较为浪费。
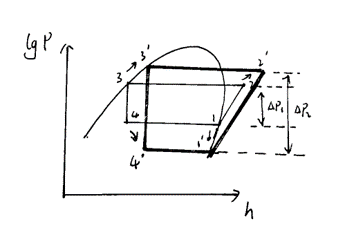
需要注意的是,当认为系统其他部分组件保持不动时,仅仅调节转速带来的效果不仅仅是系统流速的增加,还会改变压缩机压缩比,其原本的循环将会改变,如下图所示。因此,其循环效率的计算需要重新修正计算。
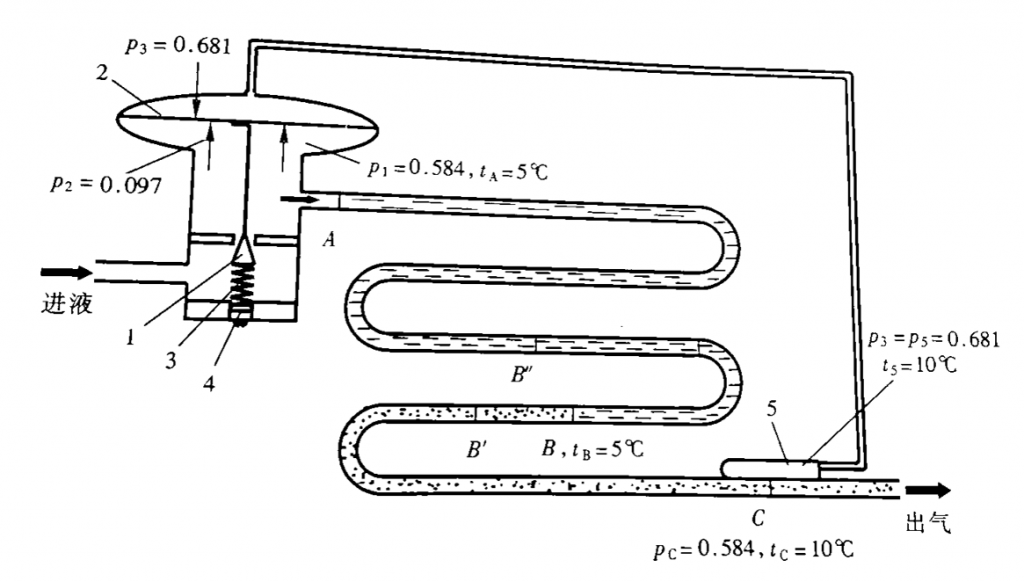
之后再关注下节流阀部分。节流阀的类型有很多,包括浮球膨胀阀、热力膨胀阀、电子膨胀阀等等,但其解决的问题就是一个,避免蒸发器内未汽化的部分制冷剂液体进入压缩机引起湿压缩造成液击的发生,因此其可以想象为一个类似于风机盘管水侧节流阀的存在,调节开度,从而调节流量,在维持蒸发器侧蒸发压力不变的条件下,适应变化的负荷。
在两器处也有控制机构可以进行调节,包括蒸发压力调节阀、压缩机吸气压力调节阀、冷凝压力调节阀,在我看来,它们与节流阀起到的作用是类似的,都是控制蒸发器压力,只是作用的位置不同,这里很大可能不对,但目前就理解到这。
可以看出,在部分负荷下,制冷循环的的变化是需要以情形而定的,如果系统压缩比不变,并且蒸发压力冷凝压力不变,那么皆大欢喜,在两器温度不变的工况下修正一个参数即可,但倘若系统压缩比变化,整个系统的变化,外界两器温度不变的情况下,制冷剂两器处的温度还会发生变化,还需要对各个负荷工况进行修正,看起来是较为麻烦的,对机理模型的搭建是一个挑战。
卡诺冷机
卡诺冷机是以卡诺循环理论为基础进行搭建的,库中提供了两个模型,一个是利用部分负荷率控制的模型(Buildings.Fluid.Chillers.Carnot_y),另一个是利用蒸发器出口温度控制的模型(Buildings.Fluid.Chillers.Carnot_TEva)。两个模型在搭建过程中,利用到了分层建模的思想,先按照逆卡诺循环的机理搭建了基础模块(Buildings.Fluid.Chillers.BaseClasses.Carnot),然后借助该模块拓展出两个模型。
首先介绍一下基础模块:Buildings.Fluid.Chillers.BaseClasses.Carnot,其中,我将其中关键的几段代码摘出,如下,其实就是对几个效率进行了定义,包括名义上的逆卡诺循环效率以及修正后的COP系数,可以看出其中的逆卡诺循环系数是利用蒸发器、冷凝器出口温度,再加上两器接近温度的影响后计算得到的,COP的计算则利用了两个修正,一个是类似于满载负荷下的修正,也就是满载负荷下,实际COP与理论COP之间的比值,另外一个是部分负荷率(yPL)下的修正。
Real yPL(final unit="1", min=0) = if COP_is_for_cooling
then QEva_flow/QEva_flow_nominal
else QCon_flow/QCon_flow_nominal "Part load ratio";
Real etaPL(final unit = "1")=
if evaluate_etaPL
then Buildings.Utilities.Math.Functions.polynomial(a=a, x=yPL)
else 1
"Efficiency due to part load (etaPL(yPL=1)=1)";
Real COP(min=0, final unit="1") = etaCarnot_nominal_internal * COPCar * etaPL
"Coefficient of performance";
Real COPCar(min=0) = TUseAct/Buildings.Utilities.Math.Functions.smoothMax(
x1=1,
x2=TConAct - TEvaAct,
deltaX=0.25)
"Carnot efficiency";
Modelica.SIunits.Temperature TConAct(start=TCon_nominal + TAppCon_nominal)=
Medium1.temperature(staB1) + QCon_flow/QCon_flow_nominal*TAppCon_nominal
"Condenser temperature used to compute efficiency, taking into account pinch temperature between fluid and refrigerant";
Modelica.SIunits.Temperature TEvaAct(start=TEva_nominal - TAppEva_nominal)=
Medium2.temperature(staB2) - QEva_flow/QEva_flow_nominal*TAppEva_nominal
"Evaporator temperature used to compute efficiency, taking into account pinch temperature between fluid and refrigerant";
protected
parameter Real etaCarnot_nominal_internal(unit="1")=
if use_eta_Carnot_nominal
then etaCarnot_nominal
else COP_nominal/
(TUseAct_nominal / (TCon_nominal + TAppCon_nominal - (TEva_nominal - TAppEva_nominal)))
"Carnot effectiveness (=COP/COP_Carnot) used to compute COP";然后是在卡诺相关计算的基础上进一步完善模型,这时候两个模型的思路就不同了。
在以负载率为控制信号的冷机模型(Buildings.Fluid.Chillers.Carnot_y)中,利用两个加热冷却器(HeatExchangers.HeaterCooler_u)来实例化蒸发器与冷凝器模型其参数中最主要的是最大蒸发吸热量与最大冷凝散热量的编写,在模型中声明如下:
final QCon_flow_nominal= P_nominal - QEva_flow_nominal,
final QEva_flow_nominal = if COP_is_for_cooling
then -P_nominal * COP_nominal
else -P_nominal * (COP_nominal-1), Modelica.SIunits.HeatFlowRate QCon_flow_internal(start=QCon_flow_nominal)=
P - QEva_flow_internal "Condenser heat input";
Modelica.SIunits.HeatFlowRate QEva_flow_internal(start=QEva_flow_nominal)=
if COP_is_for_cooling then -COP * P else (1-COP)*P "Evaporator heat input";
Modelica.Blocks.Sources.RealExpression yEva_flow_in(
y=QEva_flow_internal/QEva_flow_nominal)
"Normalized evaporator heat flow rate"
annotation (Placement(transformation(extent={{-80,-50},{-60,-30}})));
Modelica.Blocks.Sources.RealExpression yCon_flow_in(
y=QCon_flow_internal/QCon_flow_nominal)
"Normalized condenser heat flow rate"
annotation (Placement(transformation(extent={{-80,30},{-60,50}})));因此,这个负荷率控制的模型更适用于那种依靠压缩机两端旁通的小型离心式压缩制冷机,一般的制冷剂在温度变化时,即使一直保持满负载运行,电功率也是会发生变化的。
另外一个是蒸发器出口温度控制的卡诺冷机模型(Buildings.Fluid.Chillers.Carnot_TEva),相比前者假设冷机电功率最大值为定值来说,这个模型更像是一个未完成品,其冷凝器实例化方法与负荷率控制的卡诺冷机是一致的,也是利用蒸发器吸热量与COP进行运算:
Modelica.SIunits.HeatFlowRate QCon_flow_internal(start=QCon_flow_nominal)=
P - QEva_flow_internal "Condenser heat input";
Modelica.SIunits.HeatFlowRate QEva_flow_internal(start=QEva_flow_nominal)=
if COP_is_for_cooling then -COP * P else (1-COP)*P "Evaporator heat input";
Modelica.Blocks.Sources.RealExpression yEva_flow_in(
y=QEva_flow_internal/QEva_flow_nominal)
"Normalized evaporator heat flow rate"
annotation (Placement(transformation(extent={{-80,-50},{-60,-30}})));
Modelica.Blocks.Sources.RealExpression yCon_flow_in(
y=QCon_flow_internal/QCon_flow_nominal)
"Normalized condenser heat flow rate"
annotation (Placement(transformation(extent={{-80,30},{-60,50}})));因此,这个负荷率控制的模型更适用于那种依靠压缩机两端旁通的小型离心式压缩制冷机,一般的制冷剂在温度变化时,即使一直保持满负载运行,电功率也是会发生变化的。
另外一个是蒸发器出口温度控制的卡诺冷机模型(Buildings.Fluid.Chillers.Carnot_TEva),相比前者假设冷机电功率最大值为定值来说,这个模型更像是一个未完成品,其冷凝器实例化方法与负荷率控制的卡诺冷机是一致的,也是利用蒸发器吸热量与COP进行运算:
final COP_is_for_cooling = true, final QCon_flow_nominal = -QEva_flow_nominal*(1 + COP_nominal)/COP_nominal, PEle(y=-QEva_flow/COP),
parameter Modelica.SIunits.HeatFlowRate QEva_flow_min(
max=0) = -Modelica.Constants.inf
"Maximum heat flow rate for cooling (negative)";以上便是卡诺冷机的模型,我认为两个模型在使用时,假设条件都太理想,不建议使用,虽然有了卡诺循环的理论基础,但是忽视了制冷压缩机的机理搭建,导致模型不能很好的反映现实冷机的运行。
DOE-2.1冷机
相比卡诺冷机,DOE-2.1冷机模型更容易介绍,其思路更加简单,就是既然冷机机理模型难以描述,那干脆不建了,直接用数据对照表来解决,然后做的时候发现数据是有规律的,那更好了,用规则曲线直接就描述了。因此模型的关键就在于三条修正曲线(虽然有两个模型,其实原理是相同的,只是一个认为是冷凝器进口温度影响了三条曲线,另一个认为是冷凝器出口温度影响了三条曲线)
- capFunT:满载负荷下制冷容量的修正曲线,可以理解为制冷循环中,在考虑节流损失、过热损失的背景下,对不同蒸发器温度、不同冷凝器温度下的制冷容量进行修正,将压缩机性能、卡诺循环的变化以及不同温度下制冷循环的变形都考虑在内。
- EIRFunT:满载负荷下温度修正曲线,可以理解为满载负荷率下,温度对于COP的影响,从数学表达式来看其实就是对1/cop进行修正。
- EIRFunPLR:部分负荷率下负荷率修正曲线,可以理解为部分负荷率下,对于COP的修正。
当计算时,会利用三条曲线对输出功率进行计算,模型中的计算公式如下,此外做了一些修改,使其变得更加的通俗易懂。
其中CR是用于当冷机实际负载率小于额定最小负载率时使用的,正常使用时就是1。
if on then
// Compute the chiller capacity fraction, using a biquadratic curve.
// Since the regression for capacity can have negative values (for unreasonable temperatures),
// we constrain its return value to be non-negative. This prevents the solver to pick the
// unrealistic solution.
capFunT = Buildings.Utilities.Math.Functions.smoothMax(
x1 = 1E-6,
x2 = Buildings.Utilities.Math.Functions.biquadratic(a=per.capFunT, x1=TEvaLvg_degC, x2=TConEnt_degC),
deltaX = 1E-7);
/* assert(capFunT > 0.1, "Error: Received capFunT = " + String(capFunT) + ".\n"
+ "Coefficient for polynomial seem to be not valid for the encountered temperature range.\n"
+ "Temperatures are TConEnt_degC = " + String(TConEnt_degC) + " degC\n"
+ " TEvaLvg_degC = " + String(TEvaLvg_degC) + " degC");
*/
// Chiller energy input ratio biquadratic curve.
EIRFunT = Buildings.Utilities.Math.Functions.biquadratic(a=per.EIRFunT, x1=TEvaLvg_degC, x2=TConEnt_degC);
// Chiller energy input ratio quadratic curve
EIRFunPLR = per.EIRFunPLR[1]+per.EIRFunPLR[2]*PLR2+per.EIRFunPLR[3]*PLR2^2;
else
capFunT = 0;
EIRFunT = 0;
EIRFunPLR = 0;
end if;这里解释一下这一句:“将卡诺循环的变化以及不同温度下制冷循环的变形都考虑在内”,就是说如果按照机理模型去搭建的时候,两器温度变化时,最大制冷容量的修改有三部分,第一个是卡诺效率的变化,两边温度修改,理想卡诺循环就得修改,这一点还比较容易考虑,第二个是节流损失、过热损失的重新计算,在卡诺冷机模型中,这个似乎考虑成为定值,是否合理不清楚,第三个是压缩机压差变化带来的流量变化。用一个公式避免了大量的机理,就很舒服。
冷机模型的校准工作
对于冷机模型的校准,目前对于两大类模型的校准均有涉及,这里说一下校准过程中的感受。
首先,对于第一类模型的校准(卡诺冷机)目前只在实验室冷机上校准(定频启停控制冷机),主要校准其COP与理想状况下逆卡诺循环效率的比例以及两器的接近温度,校准参数较为清晰,但不清楚在其他工况下,模型拓展性效果,用的人也比较少。
其次是两个DOE-2.1冷机,其实是有文章讲述其校准流程的,标准化的校准流程应该如下:
检查校准所需数据集是否完整,讲述DOE-2.1修正版模型中对于典型校准数据集的定义包括:
在属性维度上:
- 冷机制冷容量上限
- 冷机电功率
- 冷冻水供水温度
- 冷却水出口温度(当缺失出口温度时,也可以根据简单的热量-温度换算得到)
在时间维度上:
- 全负载率时的运行数据(注意此处的全负载率是指压缩机全功率运行,与IPLV中对于负荷率的定义是不同的,IPLV中负荷率是指与额定制冷容量的比值)
- 部分负载率下的数据
对数据集进行处理,分离出满载时的数据,处理得到容量修正系数(最大制冷量与额定制冷量的比值)与满负载下 COP 修正系数(当前工况的 COP 与额定 COP 的比值),文章中称之为中间值,然后进行拟合计算,需要注意的是EIRFunT是修正的COP的倒数,拟合的时候使用最小二乘法即可。
分离出部分负载下的数据,计算部分负载下 COP 修正系数。
进行测试,验证模型准确性,可以采用两个指标对模型准确性进行衡量,一个是 CVRMSE 指标,主要是衡量数据的分散程度,另一个是 MBE 指标,用于衡量模型预测结果的偏差情况,但在最小二乘法的作用下,MBE 将会等于0(如果训练数据与测试数据采用相同的数据集),对于CVRMSE,一般追求5%以内的误差(好像来自于,Economic uncertainties in chilled water system design,但这篇文章没下载下来):
上述是论文中常用的校准流程,但是在实际使用过程中,由于国内厂家一般不会提供较为详细的运行数据(从使用经验来看,york公司提供的数据一般还有较多运行数据,包括部分负荷率、不同工况,并且在Building库中已经大量内置了性能参数,但国内格力这种,一般数据量较少),但国内厂商一般会提供几个数据,一个是标况下IPLV测试数据,一般有4个点,100%负载率,75%负载率,50%负载率,25%负载率,另一个是非标况下IPLV测试数据,这个可能多一点,最后是COP与负载率之间的变化图。做的时候会发现,满载负荷下的两条曲线是没有办法拟合的(数据样本没有,并且IPLV的满载与冷机模型中的满载的含义是不同的),只能先从部分负载率开始校准,这时候COP与负载率之间的关系就可以进行识别,正好EIRFunPLR正好是1/COP在部分负载下的修正系数,满载COP也有,COP也有,负荷率也有,就可以拟合,此外,此处还需要注意,DOE-2.1原始版本的第三条曲线认为这个修正系数只与负载率相关,但之后修正的版本加上了冷凝器的修正,这里可以依据数据结果做一些修正,例如我这里添加了冷凝器进口温度的修正(论文中的修正模型是对冷凝器出口温度的修正但我没法得到冷凝器出口温度的测量值,这里我认为进口温度与出口温度修正意义是一样的,只有可能曲线形式不一样罢了,只要准就行),效果如下,左图只使用负载率进行修正,右图加入了冷凝器温度的修正:
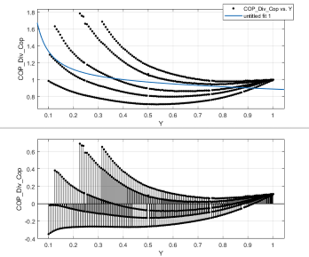
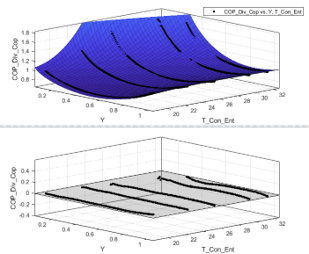
之后再对前两条曲线进行修正,样本点不够只能在其他容量相似压缩机形式一样的已有参数表上进行修改,利用仅剩的几个数据进行验证。引用其他冷机性能表这点可以在模型中进行修改,引入其他冷机的性能曲线再进行修改,从而方便便利寻找最合适的曲线,例如我修改的代码如下(这种处理方法不够严谨,仅供参考):
if on then
// Compute the chiller capacity fraction, using a biquadratic curve.
// Since the regression for capacity can have negative values (for unreasonable temperatures),
// we constrain its return value to be non-negative. This prevents the solver to pick the
// unrealistic solution.
capFunT = (Buildings.Utilities.Math.Functions.smoothMax(
x1 = 1E-6,
x2 = Buildings.Utilities.Math.Functions.biquadratic(a=per_Extends.capFunT,
x1=TEvaLvg_degC-per.TEvaLvg_nominal+per_Extends.TEvaLvg_nominal,
x2=TConEnt_degC-per.TConEnt_nominal+per_Extends.TConEnt_nominal),
deltaX = 1E-7)-1)
*0.012+1;
/* assert(capFunT > 0.1, "Error: Received capFunT = " + String(capFunT) + ".\n"
+ "Coefficient for polynomial seem to be not valid for the encountered temperature range.\n"
+ "Temperatures are TConEnt_degC = " + String(TConEnt_degC) + " degC\n"
+ " TEvaLvg_degC = " + String(TEvaLvg_degC) + " degC");
*/
// Chiller energy input ratio biquadratic curve.
EIRFunT = (Buildings.Utilities.Math.Functions.biquadratic(a=per_Extends.EIRFunT,
x1=TEvaLvg_degC-per.TEvaLvg_nominal+per_Extends.TEvaLvg_nominal,
x2=TConEnt_degC-per.TConEnt_nominal+per_Extends.TConEnt_nominal)-1)
*1.036+1;
// Chiller energy input ratio quadratic curve
EIRFunPLR = Buildings.Utilities.Math.Functions.bicubic(a=per.EIRFunPLR, x1=PLR2, x2=TConEnt_degC);展望
虽然说机理模型的搭建很复杂,但是在数据量缺乏的情况下,搭建更加机理的模型去补充数据的缺失是唯一的路径,在冷机模型中加入压缩机模型,应该比较有意思,然后尝试是否可以使用更少的数据校准冷机模型。
如何创造一个只提供很少样本点但能构造出大致合理的性能曲线,这个将对MPC通用性的提升有很大帮助。









评论
还没有任何评论,你来说两句吧!